
| M o n a r c h W a t c h | |
| Reading Room |
ROOM
Introduction
Articles
Season
Summaries
Scientific
Bibliography
Classroom
Bibliography
Frequently
Asked
Questions
| Articles : Do Female Monarchs Show Egg-Laying Preferences? | |||||||||||||||||||
|
Do Female Monarchs Show Egg-Laying Preferences? Christine Byerley, Orley R. Taylor, Stephanie Darnell In most of the Monarch’s breeding areas, there are four to fifteen species of milkweeds, all of which are potential hosts for Monarch larvae. These plants differ in many aspects, such as growth rates, toughness, hairiness, chemical make-up, and so on. This observation leads us to an interesting question about these varied plants: are they all equally attractive to Monarchs for oviposition and feeding? Let's examine the oviposition question. How could we determine if females prefer one species over another? We should start with a hypothesis. The best approach is to start with a null hypothesis (sometimes written Ho). The null hypothesis states that there is no difference between milkweed species A and B. The purpose of designing a test around a null hypothesis is to avoid the problem of unconsciously letting our expectations become part of our results. Our objective should be not to find that A is preferred more than B, if this is our expectation, but to establish in a neutral and objective way the preference or lack of preference shown by the butterflies. In other words, if we have prior knowledge, or think we do, that species A is preferred to species B, we might unintentionally obtain results which support this hypothesis. By suppressing our expectations, and doing a neutral test, we can let the butterflies tell us whether or not they show preferences. How could we conduct such a test? In the field it is very difficult to follow Monarchs and keep track of which milkweed species they use for egg laying. Even if we made such observations, it might not be possible to tell which species they prefer. We would need to be able to determine if the ratio of contacts with the plants to eggs laid differed between or among milkweed species. However, in the laboratory we can provide a choice. To test for oviposition preference, we will need mated female Monarchs (how many?), a large flight cage, artificial nectar, and at least two species of milkweed which we can use to test for oviposition. If you set up such a cage and put in one species of milkweed and record the number of eggs per hour, you will notice that most of the egg laying occurs in the first 4-5 hours of light each day. From this observation, it becomes clear that if we wish to test for preference, we should do so in the morning hours. To conduct a test Analyzing the results Interpretation of results Alternatives Add ons If students carry out the basic experiment outlined above and obtain results which indicate that females lay significantly more eggs on one type of plant, the next question is what is the underlying basis for the difference? Do the females make choices before they land on the plants or after they have made contact? This question could be examined by making careful observations and records of ratios of contact to egg laying. Remember, to facilitate observations and data collecting, Monarchs can be marked to distinguish one from another - either with the use of tags or by using a permanent marking pen to give each individual a number in the discal cell on the underside of the hindwing. EXAMPLE OUTCOMES Number of eggs laid by female Monarchs (N=20) in 15 minute intervals.
Various statistical tests can be used to ask if there is a significant difference between two observations or sets of outcomes. The Chi Square (X2) test is frequently used to determine whether differences are likely to be due to chance, referred to as sampling variability (or sampling error), or likely to occur so rarely that they represent real or significant differences between two data sets. If the differences between A and B are so small as to be due to chance, then there is no significant difference between them and we are unable to reject the null hypothesis. If, on the other hand, the difference between A and B is significant at a probability of <.05% then we can reject the null hypothesis. Steps for Performing X2 Statistics 1) State the Null Hypothesis (H0) For example, female Monarchs show no egg-laying preferences and will lay similar numbers of eggs on milkweed species A and milkweed species B. 2) Calculate ECF (Expected Cell Frequency) based on marginal frequencies from the observed data.
3) Fill the expected data table with ECFs calculated. 4) Calculate X2. The X2 formula compares expected and observed cell frequencies to measure the difference between observed and expected values. 5) Calculate degrees of freedom (d.f.)
Degrees of freedom is the number of quantities that are unknown minus the number of independent equations linking these unknowns. For a contingency table, this is the number of cells that must be filled in to determine all the cells. For example: a two by two table, the row and column marginals are known and the value in only one cell needs to be calculated to figure out all the other cells. i.e. d.f. = (2-1)(2-1)= 1 6) Select a significance level. Most often .05 level is chosen. (Significance at the .05 level means that 5 out of 100 times the differences observed may have occurred by chance). 7) Look up the X2 value on the Chi Square Distribution Table . Look at the value under the chosen significance level and the degrees of freedom calculated. 8) Check to see if the computed X2 value is greater than the table value.
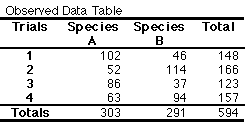
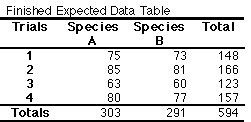
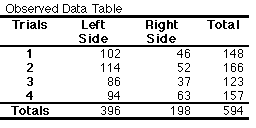
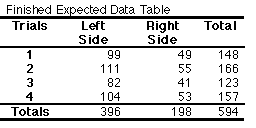
EXAMPLES USING THE GIVEN OBSERVED NUMBERS EXAMPLE 1: Is there an egg-laying preference between the two species of milkweed by the Monarch? 1) State the Null Hypothesis: There is no difference in egg laying preference between milkweed species A and B. 2) Calculate ECF, and 3) Fill the Expected Data Table The values bolded are the marginal frequencies from the observed data (or known values). Calculate the ECF for Species A - Trial 1 = (148 x 303) / 594 Calculate the rest of the ECF’s for Species A. Then finish filling in the table by simple subtraction from the totals for each row. 4) Calculate 5.) Calculate d.f. (4 - 1)(2 - 1) = 3 6) Significance level at .05 7) X2 value in table = 7.81 8) Compare the computed X2 and the X2 table value. The computed value is larger, therefore the H0 is rejected. The relationship between milkweed species A and B is statistically significant. EXAMPLE 2: Is there a position effect in the cage? 1) State the Null Hypothesis: There is no difference in preference of the plant placed on the left side or right side of the cage for egg laying. 2) Calculate ECF, and 3.) Fill the Expected Data Table Calculate the ECF for Left Side - Trial 1 = (396 x 148) / 594 Calculate the rest of the ECF’s for the Left Side. Then finish filling in the table by simple subtraction from the totals for each row. 4) Calculate 5) Calculate d.f. (4 - 1)(2 - 1) = 3 6) Significance level at .05 7) X2 value in table = 7.81 8) Compare the computed X2 and the X2 table value. The computed value is smaller, therefore failed to reject the H0. The there is no position effect of the plant placed on the left or the right side of the cage. References:
|
|
m o n a r c h @ k u . e d u |
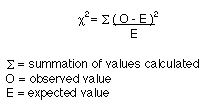

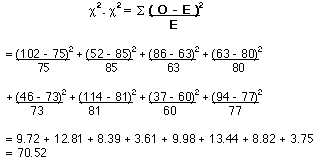
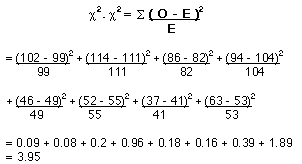
 All material on this site © Monarch Watch unless otherwise noted.
All material on this site © Monarch Watch unless otherwise noted.